Sự đa dạng của các loại tam giác khiến cho nhiều bạn băn khoăn liệu có sự khác biệt nào trong công thức tính diện tích các loại hình tam giác này hay không. Hãy cùng tìm hiểu công thức tính diện tích hình tam giác và những điều cần biết trong nội dung bài viết dưới đây!

1. Khái niệm cơ bản về hình tam giác

Cũng giống như hình vuông, hình chữ nhật thì hình tam giác là một loại hình vô cùng cơ bản trong bộ môn hình học. Ngay từ lớp 1, các bạn học sinh đã được tiếp cận với loại hình này và được giới thiệu sơ bộ những thông tin cơ bản về nó.

Theo đó, hình tam giác là loại hình tồn tại trong mặt phẳng hai chiều. Sở hữu ba đỉnh là ba điểm khác nhau và chúng không thẳng hàng. Ba cạnh của tam giác là ba đường thẳng nối liền ba đỉnh này. Và trong số tất cả các loại hình học, hình tam giác là hình có số cạnh ít nhất.

Hình tam giác là hình có 3 cạnh

Hình tam giác là hình có 3 cạnh

Một số tính chất cơ bản của tam giác như sau:

2. Có những loại tam giác nào?

Chúng ta có thể dựa vào những yếu tố như cạnh hoặc góc để phân loại các loại hình tam giác khác nhau. Hoặc sử dụng yếu tố đơn lẻ, hay sử dụng kép cả hai yếu tố để xác định được loại hình tam giác.

2.1. Phân loại tam giác nhờ độ dài các cạnh

Với phương thức này, chúng ta có thể có liệt kê một số loại tam giác như:

Tam giác thường là loại tam giác cơ bản và phổ biến nhất. Đô dài các cạnh cũng như số đo ba góc của tam giác thường là khác nhau.

Tam giác cân sẽ có hai cạnh bằng nhau và gọi là hai cạnh bên. Giao điểm hai cạnh bên sẽ tạo thành đỉnh của tam giác cân. Hai góc đáy của tam giác cân sẽ bằng nhau.

Tam giác đều có cả ba cạnh bằng nhau. Ba góc trong của tam giác cân cũng bằng nhau và bằng 60 độ.

Phân loại hình tam giác

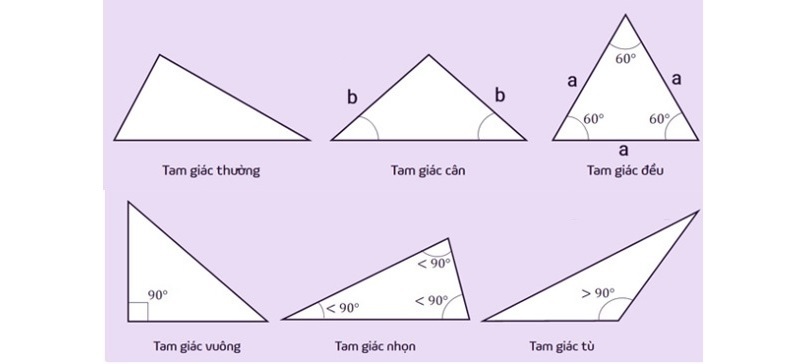
Phân loại hình tam giác

2.2. Phân loại tam giác nhờ số đo các góc

Dựa vào số đo các góc trong tam giác, ta sẽ có những loại tam giác sau:

Trong tam giác vuông sẽ có 1 góc vuông số đo 90 độ. Cạnh đối diện với góc vuông đó gọi là cạnh huyền với độ dài lớn nhất so với hai cạnh góc vuông còn lại.

Tam giác được gọi là tam giác tù khi nó sở hữu một góc trong bất kỳ có số đo trên 90 độ. Hoặc có thể nói nếu như tam giác có một góc ngoài nhỏ hơn 90 độ thì gọi là tam giác tù.

Tam giác nhọn có cả ba góc trong đều nhỏ hơn số đo 90 độ. Nghĩa là tất cả góc ngoài của tam giác đều lớn hơn 90 độ.

Tam giác vuông cân có đầy đủ tính chất của cả tam giác vuông và tam giác cân. Nghĩa là hai cạnh góc vuông sẽ có chiều dài bằng nhau. Đồng thời, hai góc nhọn đều có số đo là 45 độ.

3. Công thức tính diện tích hình tam giác và những điều cần biết

Trước khi tìm hiểu về công thức tính diện tích hình tam giác và những điều cần biết thì chúng ta cần phải xác định được đường cao cũng như đáy của tam giác đó. Bởi trong công thức tính diện tích tam giác tiêu chuẩn, đây là hai yếu tố cực kỳ quan trọng.

Công thức tính diện tích tam giác

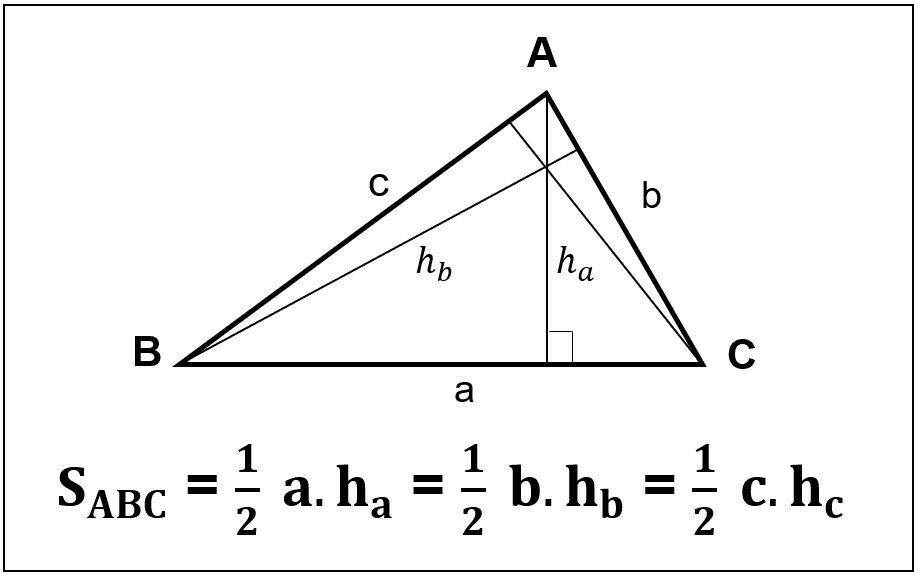
Công thức tính diện tích tam giác

Theo đó, trong một tam giác, đường hạ từ một đỉnh xuống cạnh đối diện của góc đó tạo ra một góc vuông được gọi là đường cao. Nghĩa là một đoạn thẳng trong tam giác sẽ được gọi là đường cao nếu nó được hạ từ một góc bất kỳ xuống cạnh đối diện và vuông góc với cạnh này. Và một tam giác sẽ có duy nhất 3 đường cao.

Để tính được diện tích của tam giác, chúng ta cần phải xác định được chính xác số đo chiều cao tam giác và cạnh đáy đối diện của nó. Trong đó, yếu tố chiều cao nếu như chưa được cung cấp một cách cụ thể thì chúng ta sẽ phải áp dụng các biện pháp để tạo ra nó và tính toán, đo đạc được số đo của nó.

Công thức tính diện tích hình tam giác như sau:

S = (a * h) /2

Với:

Chúng ta có thể áp dụng công thức trên cho tất cả các loại hình tam giác khác nhau. Tuy nhiên, với những tam giác đặc biệt như tam giác vuông, tam giác đều… thì việc tính toán ra các thông số sẽ đơn giản và dễ dàng hơn.

Kết luận

Trên đây là một số thông tin liên quan đến công thức tính diện tích hình tam giác và những điều cần biết. Mong rằng bài viết đã giúp các bạn phần nào củng cố được những kiến thức cơ bản liên quan đến vấn đề này. Chúc các bạn học tập, công tác tốt.